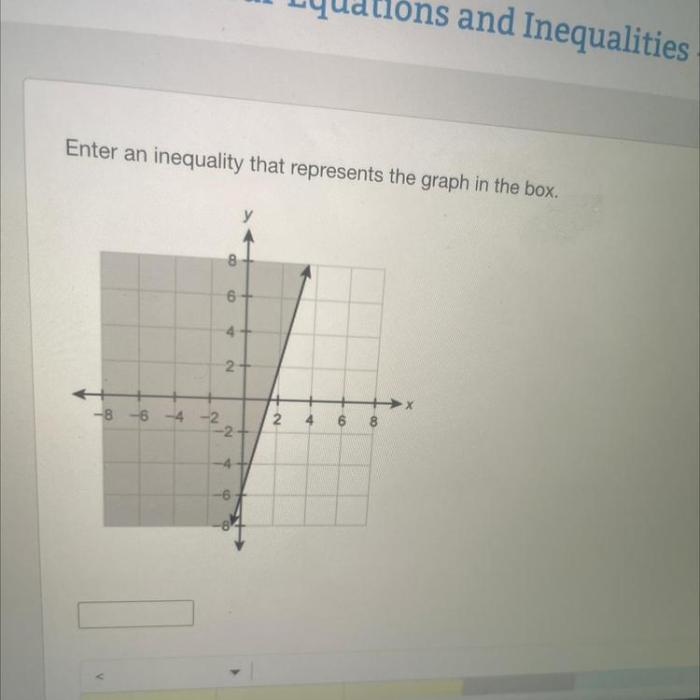
Enter an inequality that represents the graph in the box. – In the realm of mathematics, inequalities serve as powerful tools for expressing relationships between quantities. They allow us to represent a wide range of scenarios, from simple comparisons to complex mathematical models. In this article, we delve into the concept of inequalities, exploring their types, graphical representations, and practical applications.

When dealing with inequalities, it is essential to understand their fundamental concept. An inequality is a mathematical statement that compares two expressions, indicating whether one is greater than, less than, or equal to the other. Inequalities are commonly expressed using symbols such as <, >, ≤, and ≥.

1. Understanding Inequality

Inequality is a mathematical statement that compares two expressions and determines whether they are equal, greater than, or less than each other. Inequalities are used to represent relationships between variables and to solve problems in various fields, including mathematics, science, and economics.

There are three main types of inequalities:

• Less than inequality:x < y, which means x is less than y.
• Greater than inequality:x > y, which means x is greater than y.
• Less than or equal to inequality:x ≤ y, which means x is less than or equal to y.

Greater than or equal to inequality (x ≥ y) is also used to represent the relationship between x and y.

2. Representing Inequalities on a Graph

Inequalities can be represented on a graph by shading the region that satisfies the inequality.

For example, the inequality x < 2 can be represented on a graph by shading the region to the left of the vertical line x = 2.

The shaded region represents the solution set of the inequality, which is the set of all values of x that satisfy the inequality.

3. Writing Inequalities from a Graph

To write an inequality from a given graph, first identify the boundary line, which is the line that separates the shaded region from the unshaded region.

Next, determine whether the shaded region is above or below the boundary line.

If the shaded region is above the boundary line, the inequality is a greater than inequality (x > y).

If the shaded region is below the boundary line, the inequality is a less than inequality (x < y).

If the boundary line is included in the shaded region, the inequality is a less than or equal to inequality (x ≤ y) or a greater than or equal to inequality (x ≥ y).

4. Applications of Inequalities

Inequalities have numerous applications in real-world scenarios, including:

• Optimization:Inequalities can be used to find the maximum or minimum value of a function.
• Constraint satisfaction:Inequalities can be used to represent constraints in a problem and to find solutions that satisfy those constraints.
• Modeling:Inequalities can be used to model real-world phenomena, such as the motion of objects or the growth of populations.

Key Questions Answered: Enter An Inequality That Represents The Graph In The Box.

What is the difference between an equation and an inequality?

An equation states that two expressions are equal, while an inequality compares two expressions and indicates whether one is greater than, less than, or equal to the other.

How do I graph an inequality?

To graph an inequality, first identify the boundary line, which is the line that separates the two regions of the graph. Then, shade the region that satisfies the inequality.

How do I write an inequality from a graph?

To write an inequality from a graph, first identify the boundary line and the shaded region. The inequality will be based on the relationship between the boundary line and the shaded region.